miércoles, 30 de octubre de 2019

martes, 29 de octubre de 2019

El algoritmo de Dijkstra te permite calcular la ruta más corta entre un nodo (tú eliges cuál) y todos los demás nodos en el grafo. Encontrarás una descripción del algoritmo al final de esta página, pero ¡vamos a estudiarlo con un ejemplo explicado! Calcularemos la distancia más corta entre el nodo C y los demás nodos del grafo:

Durante la ejecución del algoritmo, iremos marcando cada nodo con su distancia mínima al nodo C (nuestro nodo elegido). Para el nodo C, esta distancia es 0. Para el resto de nodos, como todavía no conocemos esa distancia mínima, empieza siendo infinita (∞):

También tendremos un nodo actual. Inicialmente, el nodo actual será C (nuestro nodo elegido). En la imagen, marcaremos el nodo actual con un punto rojo.

Ahora, revisaremos los vecinos de nuestro nodo actual (A, B y D) en cualquier orden. Empecemos con B. Sumamos la mínima distancia del nodo actual (en este caso, 0) con el peso de la arista que conecta al nodo actual con B (en este caso, 7), y obtenemos 0 + 7 = 7. Comparamos ese valor con la mínima distancia de B (infinito); el valor más pequeño es el que queda como la distancia mínima de B (en este caso, 7 es menos que infinito):

Bien. Ahora revisaremos al vecino A. Sumamos 0 (la distancia mínima de C, nuestro nodo actual) con 1 (el peso de la arista que conecta nuestro nodo actual con A) para obtener 1. Comparamos ese 1 con la mínima distancia de A (infinito) y dejamos el menor valor:

OK. Repetimos el procedimiento para D:

Genial. Hemos revisado todos los vecinos de C. Por ello, lo marcamos como visitado. Representemos a los nodos visitados con una marca de verificación verde:

Ahora debemos seleccionar un nuevo nodo actual. Ese nodo debe ser el nodo no visitado con la menor distancia mínima, es decir, el nodo con el menor número y sin marca de verificación verde. En este caso, ese nodo es A. Vamos a marcarlo con el punto rojo:

Ahora, repetimos el algoritmo. Revisamos los vecinos de nuestro nodo actual, ignorando los visitados. Esto significa que solo revisaremos B.

Para B, sumamos 1 (la distancia mínima de A, nuestro nodo actual) con 3 (el peso de la arista conectando a A con B) para obtener 4. Comparamos ese 4 con la distancia mínima de B (7) y dejamos el menor valor: 4.

Después, marcamos A como visitado y elegimos un nuevo nodo: D, que es el nodo no visitado con la menor distancia mínima.

Repetimos el algoritmo de nuevo. Esta vez, revisamos B y E.

Para B, obtenemos 2 + 5 = 7. Comparamos ese valor con la distancia mínima de B (4) y dejamos el menor valor (4). Para E, obtenemos 2 + 7 = 9, lo comparamos con la distancia mínima de E (infinito) y dejamos el valor menor (9).

Marcamos D como visitado y establecemos nuestro nodo actual en B.

Casi terminamos. Sólo debemos verificar E. 4 + 1 = 5, que es menos que la distancia mínima de E (9), así que dejamos el 5. Marcamos B como visitado y establecemos E como el nodo actual.

E no tiene vecinos no visitados, así que no verificamos nada. Lo marcamos como visitado.

Como no hay nodos no visitados, ¡terminamos! La distancia mínima de cada nodo ahora representa la mínima distancia entre ese nodo y el nodo C (el nodo que elegimos como nodo inicial).

Aquí está una descripción del algoritmo:

Marca el nodo inicial que elegiste con una distancia actual de 0 y el resto con infinito.
Establece el nodo no visitado con la menor distancia actual como el nodo actual A.
Para cada vecino V de tu nodo actual A: suma la distancia actual de A con el peso de la arista que conecta a A con V. Si el resultado es menor que la distancia actual de V, establécese como la nueva distancia actual de V.
Marca el nodo actual A como visitado.
Si hay nodos no visitados, ve al paso 2.

miércoles, 23 de octubre de 2019

Capturas Ejercicio Método Transporte

domingo, 13 de octubre de 2019

Ejercicio

miércoles, 9 de octubre de 2019

Método de Transporte de Vogel

Método de Aproximación de Vogel (Algoritmo de Transporte en Programación Lineal)

El Método de Aproximación de Vogel es una versión mejorada del Método del Costo Mínimo y el Método de la Esquina Noroeste que en general produce mejores soluciones básicas factibles de inicio, entendiendo por ello a soluciones básicas factibles que reportan un menor valor en la función objetivo (de minimización) de un Problema de Transporte balanceado (suma de la oferta = suma de la demanda).

Los pasos que requiere la aplicación del Método de Aproximación de Vogel son los siguientes:

Paso 1: Determinar para cada fila (columna) una medida de penalización restando el elemento de costo unitario mínimo en la fila (columna) del elemento con costo unitario siguiente al mínimo de la misma fila (columna).

Paso 2: Identificar la fila o columna con la mayor penalización. Romper los empates (de existir) de forma arbitraria. Asignar todo lo posible a la variable que tenga el mínimo costo unitario de la fila o columna seleccionada. Ajusta la oferta y la demanda y tachar la fila o la columna ya satisfecha. Si se satisfacen una fila y una columna en forma simultánea, sólo se tacha uno de los dos y al que queda se le asigna oferta o demanda cero.

Paso 3:

Si queda sin tachar exactamente una fila o columna con cero oferta o demanda, detenerse.
Si queda sin tachar una fila (columna) con oferta (demanda) positiva, determinar las variables básicas en la fila (columna) con el Método del Costo Mínimo. Detenerse.
Si todas las filas y columnas que no se tacharon tienen cero oferta y demanda (restante), determinar las variables básicas cero por el Método del Costo Mínimo. Detenerse.
En cualquier otro caso, seguir en el Paso 1.

Ejemplo Método de Aproximación de Vogel

Consideremos nuevamente un problema de transporte balanceado que tiene 3 fuentes de oferta (silos) y 4 fuentes de demanda (molinos). Los valores numéricos en la esquina superior derecha de cada cuadro, en adelante 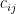$c_{ij}$ representan el costo unitario de transporte desde el silo i al molino j. Por ejemplo $c_{11}=10$ es el costo unitario de transporte desde el silo 1 al molino 1.

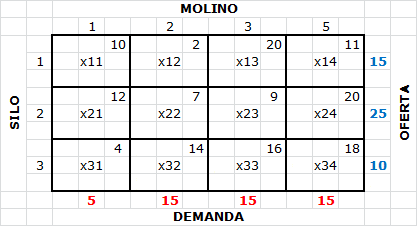
Según lo descrito anteriormente el primer paso consiste en calcular el factor de penalización para cada fila y columna de la tabla que representa el problema de transporte anterior. Por ejemplo, en la fila 1 el mínimo costo es $2 y y el costo unitario siguiente al mínimo es $10. En consecuencia la penalización de dicha fila es $8 ($10-$2). Se replica el mismo cálculo para cada fila y columna de la tabla lo cual es trivial y reporta los siguientes resultados (se han marcado las penalizaciones de las respectivas filas y columnas con color naranjo para mayor claridad):

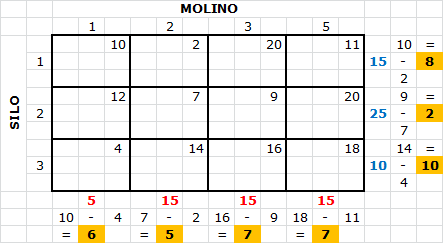
Como la fila 3 tiene la máxima penalización ($10) y la celda correspondiente a 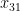$x_{31}$ tiene el costo unitario mínimo de esa fila, se asigna 5 unidades a $x_{31}$ (más no es necesario aún cuando la capacidad del silo 3 lo permite dado que la demanda del molino 1 es de sólo 5 unidades). Con esto la columna 1 se debe tachar (lo hemos marcado con color amarillo) y se procede a calcular las nuevas penalizaciones como se aprecia a continuación:

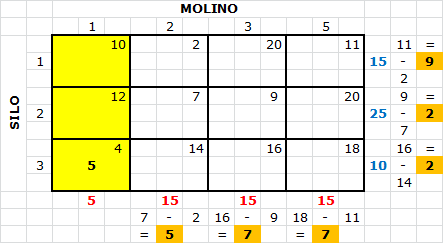
Ahora la penalización máxima es $9 ($11-$2) lo cual se alcanza en la fila 1. En consecuencia se asigna la máxima cantidad posible a la variable $x_{12}$ , con lo que se obtiene $x_{12}=15$ , y al mismo tiempo se satisfacen tanto la fila 1 como la columna 2. En forma arbitraria se tacha la columna 2 y se ajusta a cero la oferta en la fila 1.

Al continuar de la misma forma, ahora la fila 2 es la que produce la máxima penalización correspondiente a $11 ($20-$9), por tanto se asigna $x_{23}=15$ , con lo que se tacha la columna 3 y quedan 10 unidades en la fila 2. Sólo queda la columna 4 y tiene 15 unidades de oferta positiva. Al aplicar el Método del Costo Mínimo a esa columna, se asigna de forma sucesiva $x_{14}=0, x_{34}=5, x_{24}=10$ (se recomienda verificar dichos resultados). Notar adicionalmente que hay otras soluciones posibles que dependen de cómo se rompen los empates.

El valor de la función objetivo asociado a esta solución factible inicial es Z=15(2)+0(11)+15(9)+10(20)+5(4)+5(18)=$475 que es similar a lo alcanzado por el Método del Costo Mínimo, no obstante, en general el Método de Aproximación de Vogel reporta mejor solución de inicio.